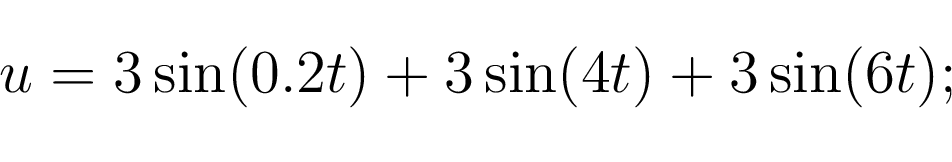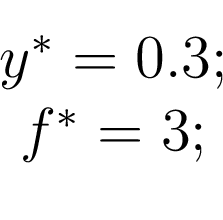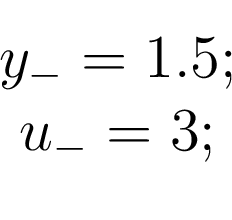Пакет "Автоматика"
Пакет программ "Автоматика" в среде Matlab служит для автоматизации построения алгоритмов работы регуляторов сложных одномерных и многомерных объектов. Он предназначен для разработчиков реальных систем автоматического управления.
A. Цели управления
- Точность
Она определяется заданными допусками на ошибки регулирования по каждой регулируемой переменной. - Время регулирования
B. Исходные данные
- Линеаризованные дифференциальные уравнения объекта управления в различных формах (пространство состояния, "вход-выход", передаточная матрица)
- Внешние возмущения и
помехи
Они являются неизвестными кусочно-непрерывными функциями с известными ограничениями их изменения. - Неопределенность
коэффициентов объекта
Выделяют две степени неопределенности. Малая степень, когда существует регулятор, обеспечивающий достижение заданных целей управления для всех возможных значений коэффициентов из заданных диапазонов (робастная стабилизация). Большая степень неопределенности соответствует случаю, когда такого регулятора не существует и алгоритм работы регулятора зависит от реализовавшихся значений коэффициентов объекта.При малой степени неопределенности признаком сохранения точности и времени регулирования в пакете служат запасы устойчивости по фазе и модулю. При большой степени неопределенности пакет формирует адаптивное управление.
C. Работа с пакетом
Пакет состоит из директив, решающих определенные классы задач. Эти классы образуются в зависимости от свойств объекта (минимально- либо неминимально-фазовые объекты и т. п.), степени неопределенности его коэффициентов, уровня внешних возмущений и т. п. Директива содержит интерфейс и расчетную часть. Интерфейс служит для ввода исходных данных и вывода результатов директивы.
Пакет содержит три группы директив: синтез регуляторов, конечно-частотная идентификация, частотное адаптивное управление.
Работать с пакетом просто. Разработчик системы автоматического управления выбирает из списка директив ту, которая решает его задачу, вводит, используя интерфейс, исходные данные и получает результат: алгоритм работы регулятора и графики моделирования процесса управления с этим регулятором.
D. Область применения
Применение пакета не зависит от физической природы объекта управления. Требуется лишь, чтобы сведения о нем могли быть представлены в форме п. B.
E. Состояние пакета
Пакет является развитием наших пакетов ГАММА-1PC (1997 г.) и ADAPLAB-3 (2009 г.). Первый из них разработан вне среды Matlab и его разработка под названием ГАММА-2 продолжается.
Пакет ГАММА-1PC использовался для построения алгоритмов работы регуляторов различных объектов таких как: гироскопическая платформа, газовый коллектор месторождения, сложная энергетическая система и т. п.
Пакет ADAPLAB-3, разработанный в среде Matlab, использовался для построения адаптивного регулятора системы термостабилизации устройства космического назначения.
Пакет "Автоматика" разработан для SISO объектов и MIMO объектов с двумя измеряемыми переменными и двумя управлениями. Планируется развитие пакета для большого числа измеряемых переменных и управлений.
F. Преимущества
В системе Matlab имеются пакеты для синтеза регуляторов
(Control System Toolbox) и идентификации (System Identification
Toolbox). Для синтеза регуляторов используются методы ![]() -
и
-
и ![]() -оптимизации.
Целью управления в этих методах: значение квадратичного функционала,
либо
-оптимизации.
Целью управления в этих методах: значение квадратичного функционала,
либо ![]() -норма
передаточной матрицы системы. При этом внешние возмущения и помехи
предполагаются затухающими функциями. Преимущество
пакета "Автоматика" состоит в реализации целей управления
(в условиях незатухающих внешних возмущений и помех), которые обычно
используются при разработке реальных систем. Эти преимущества основаны
на связях целей управления с коэффициентами функционалов
-норма
передаточной матрицы системы. При этом внешние возмущения и помехи
предполагаются затухающими функциями. Преимущество
пакета "Автоматика" состоит в реализации целей управления
(в условиях незатухающих внешних возмущений и помех), которые обычно
используются при разработке реальных систем. Эти преимущества основаны
на связях целей управления с коэффициентами функционалов ![]() -
и
-
и ![]() -оптимизаций, что
позволяет применить уравнения Риккати для достижения целей п. A.
Пакет System Identification Toolbox применим в ситуациях, когда внешние
возмущения отсутствуют, либо они являются белым шумом. Это относится к
частотным методам и методам наименьших квадратов. Метод
инструментальных переменных может применяться для более широкого класса
внешних возмущений. Однако в нем отсутствует самонастройка входного
сигнала, что может приводить большому времени идентификации, что может
быть недопустимо при адаптивном управлении. Преимущество
пакета "Автоматика" состоит в идентификации в условиях
почти произвольных ограниченных внешних возмущений и помех.
Это преимущество достигается путем использования частотной
идентификации с самонастройкой испытательного сигнала.
-оптимизаций, что
позволяет применить уравнения Риккати для достижения целей п. A.
Пакет System Identification Toolbox применим в ситуациях, когда внешние
возмущения отсутствуют, либо они являются белым шумом. Это относится к
частотным методам и методам наименьших квадратов. Метод
инструментальных переменных может применяться для более широкого класса
внешних возмущений. Однако в нем отсутствует самонастройка входного
сигнала, что может приводить большому времени идентификации, что может
быть недопустимо при адаптивном управлении. Преимущество
пакета "Автоматика" состоит в идентификации в условиях
почти произвольных ограниченных внешних возмущений и помех.
Это преимущество достигается путем использования частотной
идентификации с самонастройкой испытательного сигнала.
G. Примеры
G1. Синтез регуляторов
Все директивы пакета "Автоматика" решают задачи точного управления. Рассмотрим асимптотически устойчивую систему управления:
где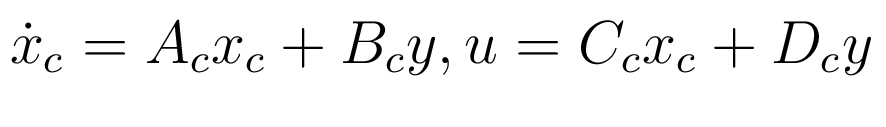
(2) 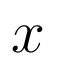 - вектор состояний объекта (1),
- вектор состояний объекта (1), 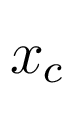 - вектор состояния регулятора (2),
- вектор состояния регулятора (2),
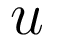 - вектор
управления,
- вектор
управления, 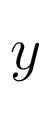 - вектор измеряемых переменных,
- вектор измеряемых переменных,  - вектор регулируемых переменных,
- вектор регулируемых переменных, 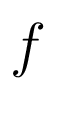 - вектор неизмеряемых внешних возмущений,
- вектор неизмеряемых внешних возмущений, 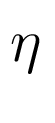 - вектор помех измерений,
- вектор помех измерений,
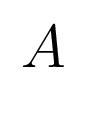 ,
,
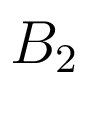 ,
, 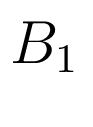 ,
,
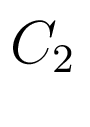 ,
, 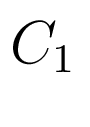 ,
,
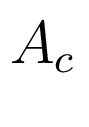 ,
, 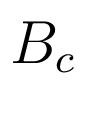 ,
,
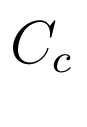 ,
, 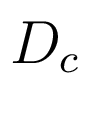 - матрицы чисел.
Внешнее возмущение и помеха измерения - ограниченные полигармонические
функции:
где частоты
- матрицы чисел.
Внешнее возмущение и помеха измерения - ограниченные полигармонические
функции:
где частоты 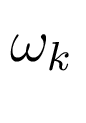 и
и 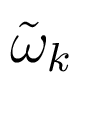 и фазы
и фазы 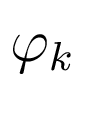 и
и 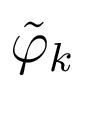
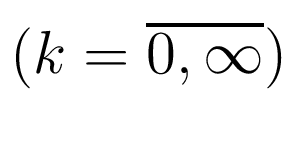 -
неизвестны, а неизвестные амплитуды
-
неизвестны, а неизвестные амплитуды 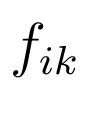 и
и 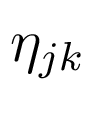
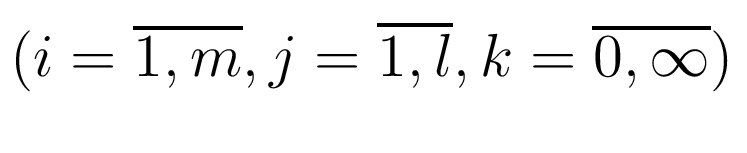 удовлетворяют
условиям:
где
удовлетворяют
условиям:
где 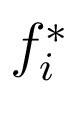 и
и 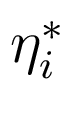
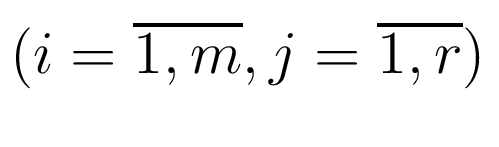 -
известные числа.
При выполнении условий (4)
справедливы неравенства:
Частным случаем функций (3)
являются кусочно-непрерывные функции, разложенные в ряд Фурье,
удовлетворяющий условиям (4).
Установившиеся ошибки по регулируемым переменным и управлениям
определим как:
Цель управления имеет вид:
где
-
известные числа.
При выполнении условий (4)
справедливы неравенства:
Частным случаем функций (3)
являются кусочно-непрерывные функции, разложенные в ряд Фурье,
удовлетворяющий условиям (4).
Установившиеся ошибки по регулируемым переменным и управлениям
определим как:
Цель управления имеет вид:
где 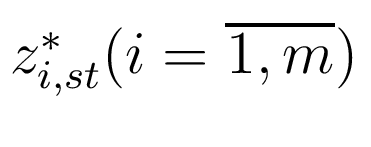 - заданные числа.
Управление, обеспечивающее достижение цели (7)
называется точным управлением.
Директивы синтеза предназначены для нахождения матриц регулятора (2), при которых достигается
цель управления (7) для объекта (1) при различных уровнях
неопределенности его матриц.
- заданные числа.
Управление, обеспечивающее достижение цели (7)
называется точным управлением.
Директивы синтеза предназначены для нахождения матриц регулятора (2), при которых достигается
цель управления (7) для объекта (1) при различных уровнях
неопределенности его матриц.
На рисунке 1 изображен интерфейс директивы синтеза регулятора для объекта заданного уравнением вида (1), где матрицы объекта имеют вид:
![$\displaystyle B_{2} = \left[ \begin{array}{c c} 1.25 & 3.75\\ 5.5 & 19.65\\...
...5\\ 0 & 0.75\\ 13.33 & 20\\ 53.33 & 2\\ 40 & 0\\ \end{array} \right]$](/images/automatica/img39.png)
(9) ![$\displaystyle B_{1} = \left[ \begin{array}{c c} 1.25 & 0\\ 5.5 & 0\\ 2 & 0\\ 0 & 0\\ 0 & 20\\ 0 & 2\\ 0 & 0\\ \end {array} \right]$](/images/automatica/img40.png)
(10) ![$\displaystyle C_{1} = C_{2}= \left[ \begin{array}{c c c c c c c} 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 1\\ \end {array} \right]$](/images/automatica/img41.png)
(11) Внешнее возмущение следующее:![$\displaystyle D = \left[ \begin{array}{c c} 0 & 0\\ 0 & 0\\ \end{array} \right]$](/images/automatica/img42.png)
(12) Рис. 2: Интерфейс программы синтеза регулятора 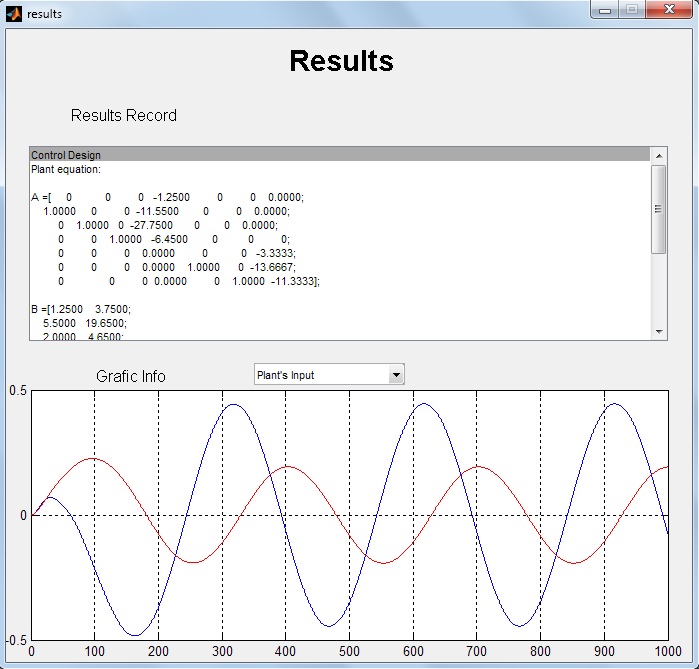
Требуемые установившиеся ошибки регулируемой пременной и границы возмущений следующие:
Значения параметров по умолчанию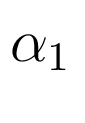 и
и 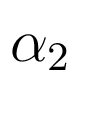 равны 3.
равны 3.
Результаты выполнения директивы показаны на рис. 2. Синтезированный регулятор (2) описывается следующими матрицами:
![$\displaystyle A_{c} = \left[ \begin{array}{c c c c c c c c c} 0 & 0 & 0 & -70...
...& 1 & 0 & -683\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 & -73\\ \end{array} \right]$](/images/automatica/img47.png)
(15) ![$\displaystyle B_{c} = \left[ \begin{array}{c c} -1431 & -5649\\ -1832 & -25...
...3933 & -18475\\ -03141 & -1429\\ -450 &0\\ 0 & 0\\ \end{array} \right]$](/images/automatica/img48.png)
(16) ![$\displaystyle C_{c}= \left[ \begin{array}{c c c c c c c c c} 0 & 0 & 0 & 1 & 0 & 0 & 0 &0 &0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 &0 &1\\ \end {array} \right]$](/images/automatica/img49.png)
(17) ![$\displaystyle D_{c} = \left[ \begin{array}{c c} 0 & 0\\ 0 & 0\\ \end{array} \right]$](/images/automatica/img50.png)
(18) G2. Конечно-частотная идентификация
Директивы конечно-частотной идентификации предназначены для моделирования процессов конечно-частотной идентификации и уточнения параметров алгоритмов идентификации. В методе конечно-частотной идентификации используются испытательные сигналы, которые являются суммой гармоник, число которых не превышает размерности вектора состояний объекта. Директивы отличаются самонастройкой амплитуд, частот и длительностью тестовых сигналов. Рассмотрим асимптотически устойчивый объект вида 1, запишем его в форме передаточных матриц:
где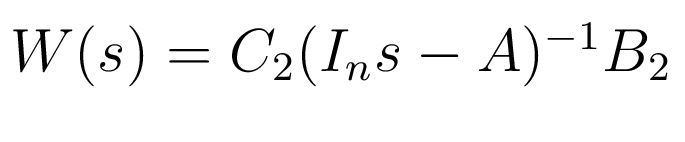 ,
,
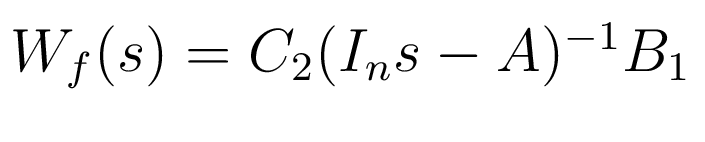 Элементы передаточной матрицы
Элементы передаточной матрицы 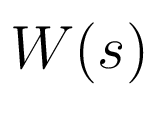 имеют вид:
Числа
имеют вид:
Числа 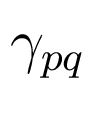 и
и 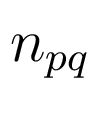 определяют
порядок передаточных матриц и могут использоваться для исследования
структурной неопределенности объекта.
К объекту 19 прикладывается
сигнал
где
определяют
порядок передаточных матриц и могут использоваться для исследования
структурной неопределенности объекта.
К объекту 19 прикладывается
сигнал
где 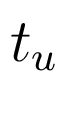 - момент приложения тестового
сигнала,
- момент приложения тестового
сигнала, 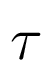 - длительность
приложения испытательного сигнала (время идентификации), частоты
- длительность
приложения испытательного сигнала (время идентификации), частоты 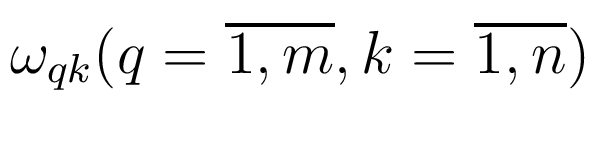 - положительные, не совпадающие друг с другом числа, амплитуды
- положительные, не совпадающие друг с другом числа, амплитуды 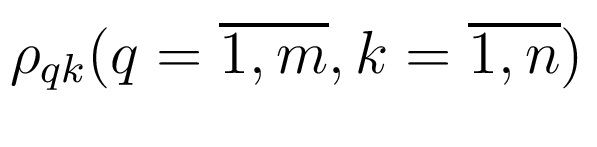 - неотрицательные числа. Директивы идентификации предназначены для
нахождения оценок коэффициентов передаточных функций 20.
Пакет производит идентификацию непрерывных и дискретных объектов.
Директивы идентификации разбиты на две группы: идентификации объектов
управления и идентификации объектов управления, замкнутых регулятором.
Алгоритмы работы директив в двух группах похожи, но для объектов,
замкнутых регулятором производится ряд дополнительных расчетов и на них
наложен ряд ограничений. Так тестовый сигнал имеет вид:
где параметры тестового сигнала
- неотрицательные числа. Директивы идентификации предназначены для
нахождения оценок коэффициентов передаточных функций 20.
Пакет производит идентификацию непрерывных и дискретных объектов.
Директивы идентификации разбиты на две группы: идентификации объектов
управления и идентификации объектов управления, замкнутых регулятором.
Алгоритмы работы директив в двух группах похожи, но для объектов,
замкнутых регулятором производится ряд дополнительных расчетов и на них
наложен ряд ограничений. Так тестовый сигнал имеет вид:
где параметры тестового сигнала 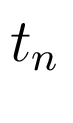 ,
,
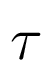 ,
,
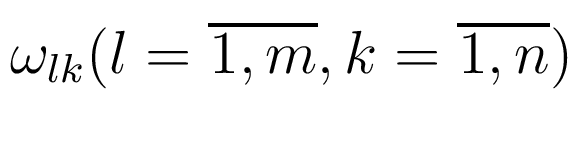 ,
,
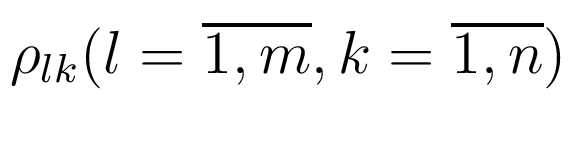 - соответствуют параметрам сигнала 21,
но задаются или настраиваются отдельно. Объект (1)
описывается уравнением
Выходы и выходы объекта и регулятора передаются на фильтр Фурье и,
используя функцию fourmi, находим значения преобразования Фурье для
входных и выходных сигналов. Затем вычисляются частотные параметры.
С помощью функции freqmi находим оценки коэффициентов передаточной
матрицы объекта 19.
- соответствуют параметрам сигнала 21,
но задаются или настраиваются отдельно. Объект (1)
описывается уравнением
Выходы и выходы объекта и регулятора передаются на фильтр Фурье и,
используя функцию fourmi, находим значения преобразования Фурье для
входных и выходных сигналов. Затем вычисляются частотные параметры.
С помощью функции freqmi находим оценки коэффициентов передаточной
матрицы объекта 19.
Пакет содержит следующие директивы идентификации:
- Директива d123sumi: идентификация без самонастройки испытательного сигнала;
- Директива d123dumi: идентификация с самонастройкой времени идентификации;
- Директива d123admi: идентификация с самонастройкой амплитуд испытательного сигнала и времени идентификации;
- Директива d123floadumi: идентификация с самонастройкой частот и амплитуд испытательного сигнала и времени идентификации.
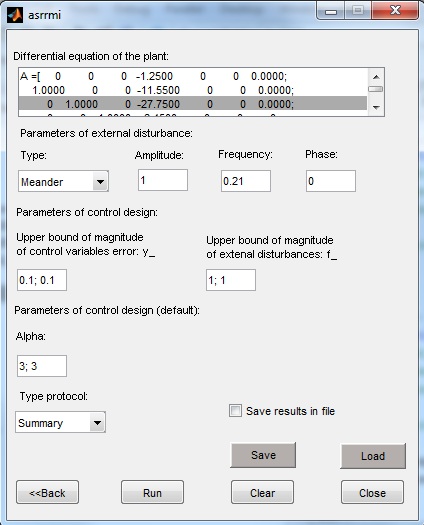
На рисунке 3 изображен интерфейс директивы идентификации без самонастройки тестового сигнала. Объект для идентификации описывается уравнением
или в виде 19 можно записать: Для объекта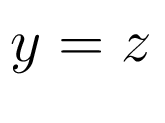 .
Далее вводятся внешние возмущения, вида:
Интервал дискретности принимается равным
.
Далее вводятся внешние возмущения, вида:
Интервал дискретности принимается равным 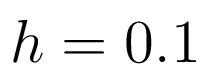 .
Далее вводятся вектора частот и амплитуд для тестового сигнала
.
Далее вводятся вектора частот и амплитуд для тестового сигнала ![$ \omega=[0.2, 4, 6]$](/images/automatica/img73.png) и
и ![$ \rho=[3, 3, 3]$](/images/automatica/img74.png) .
Таким образом тестовый сигнал примет вид:
Далее задаются параметры по умолчанию.
.
Таким образом тестовый сигнал примет вид:
Далее задаются параметры по умолчанию.
Так степени полиномов передаточных функций 19 задают структурную неопределенность объекта. По умолчанию степень полинома знаменателя передаточной функции объекта принимается
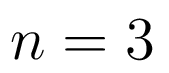 ,
также по умолчанию степень числителя принимается на единицу меньше
,
также по умолчанию степень числителя принимается на единицу меньше
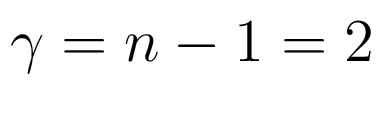 .
Параметры время идентификации и задержка начала идентификации
определяют работу директивы. Первый определяет длительность процесса
идентификации, второй - длительность переходного процесса в объекте, на
время протекания которого производится задержка начала фильтрации
сигналов. Эти параметры задаются в периодах минимальной частоты.
.
Параметры время идентификации и задержка начала идентификации
определяют работу директивы. Первый определяет длительность процесса
идентификации, второй - длительность переходного процесса в объекте, на
время протекания которого производится задержка начала фильтрации
сигналов. Эти параметры задаются в периодах минимальной частоты.
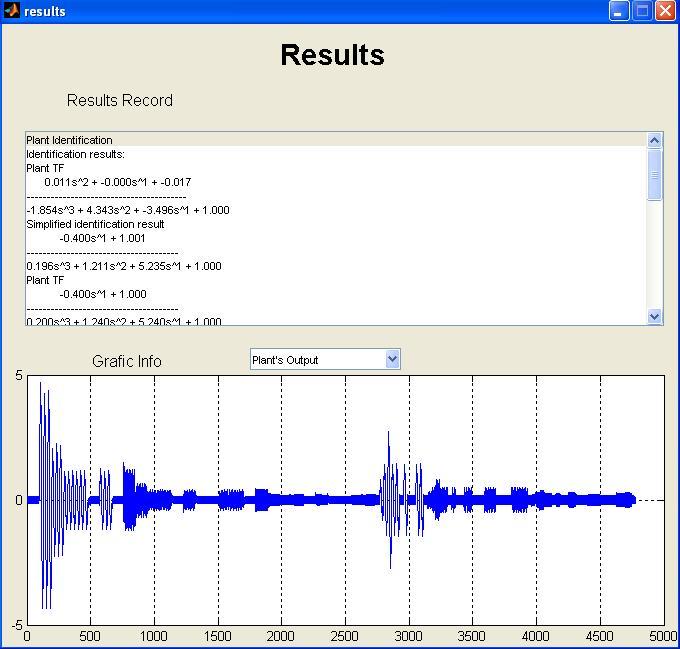
На рисунке 4 изображены результаты выполнения директивы, в верхней части окна выводится протокол выполнения директивы, а в нижнем представлена графическая информация. В таблице 1 показаны результаты идентификации.
G3. Частотное адаптивное управление
Директивы частотного адаптивного управления предназначены для моделирования процессов адаптации и уточнения параметров алгоритмов идентификации и адаптации. Директивы могут быть применены для адаптации регулятора объекта (1). Директивы адаптации имеют следующий алгоритм:
Производится идентификация объекта с помощью одной из директив идентификации объекта управления. Затем, используя одну из директив синтеза, находится регулятор (2). С течением времени коэффициенты объекта "уходят" от идентифицированных значений и точность регулятора снижается. Требуется произвести идентификацию объекта заново. Примем при этом, что система (1),(2) сохранила устойчивость. Для идентификации применяется директива идентификации объекта замкнутого регулятором. После завершения идентификации производится расчет нового регулятора для объекта. В дальнейшем при необходимости идентификация и пересчет регулятора могут выполняться необходимое число раз.
Пакет содержит следующие директивы адаптации:
- Директива d323sumi: адаптация без самонастройки испытательного сигнала;
- Директива d323dumi: адаптация с самонастройкой времени идентификации;
- Директива d323admi: адаптация с самонастройкой амплитуд испытательного сигнала и времени идентификации;
- Директива d323floadumi: адаптация с самонастройкой частот и амплитуд испытательного сигнала и времени идентификации;
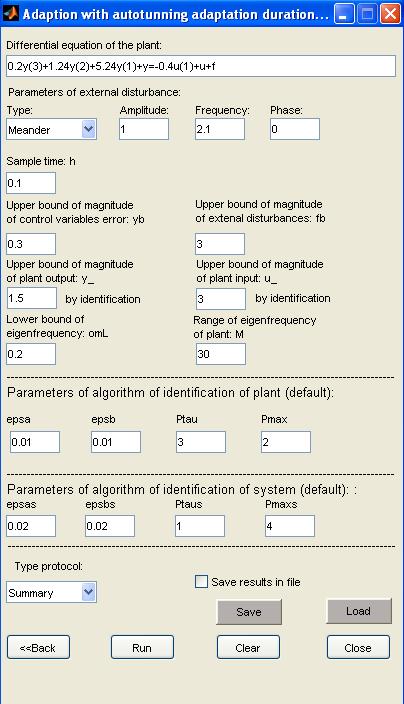
На рисунке 5 изображен интерфейс директивы адаптации с самонастройкой амплитуд тестового сигнала и времени идентификации. Объект для адаптации описывается уравнением 24 или 25, внешнее возмущение также примем равным возмущению из интерфейса идентификации 26.
Интервал дискретности принимается равным
Верхние границы входов и выходов объекта при идентификации равны: Диапазон собственных частот объекта принимается равным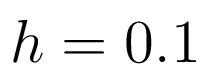 .
Требования к точности и границе внешнего возмущения определяются как:
.
Требования к точности и границе внешнего возмущения определяются как:
![$ \omega=[0.2;30.2]$](/images/automatica/img84.png) Остальные параметры задаются в интерфейсе по умолчанию, но могут быть
изменены при необходимости. Также выбирается формат протокола
директивы, есть возможность его сохранения.
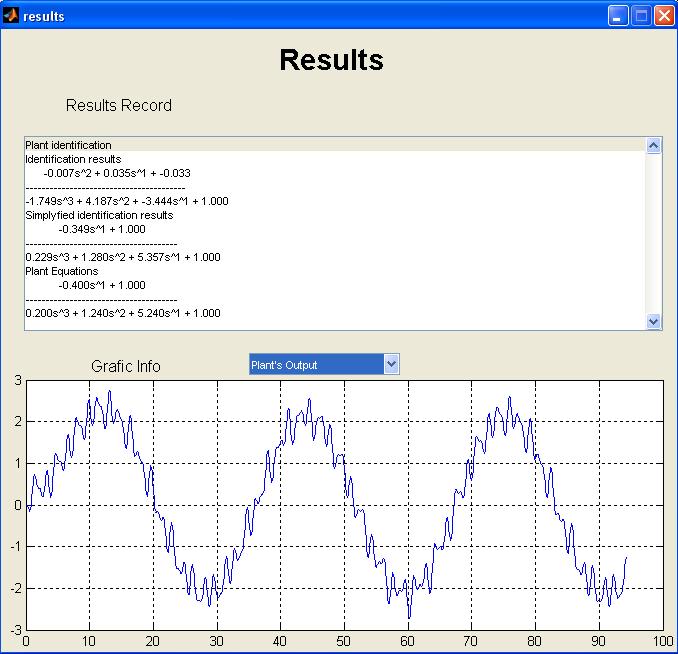
На рисунке 6
показано окно с результатами выполнения директивы.
Результаты адаптации системы представлены в таблице 2.
Остальные параметры задаются в интерфейсе по умолчанию, но могут быть
изменены при необходимости. Также выбирается формат протокола
директивы, есть возможность его сохранения.
На рисунке 6
показано окно с результатами выполнения директивы.
Результаты адаптации системы представлены в таблице 2.
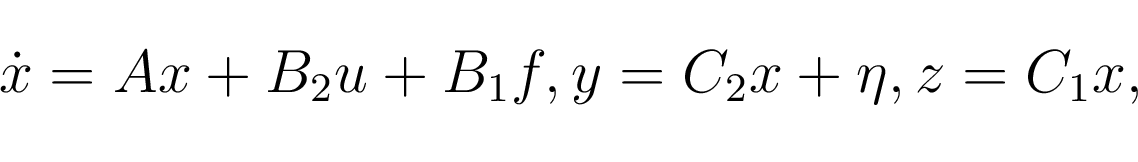
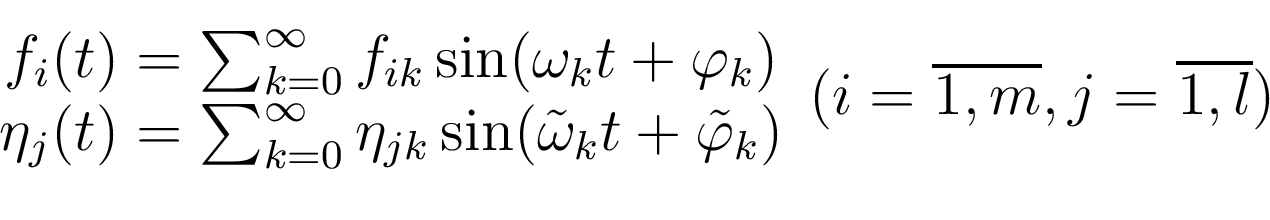
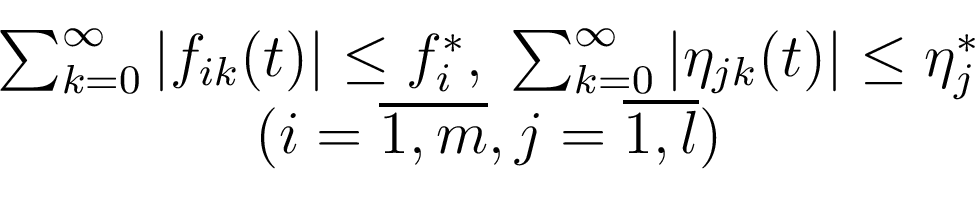
![$\displaystyle A = \left[ \begin{array}{c c c c c c c} 0 & 0 & 0 & -1.25 & 0 &...
... 0 & 1 & 0 & -13.67\\ 0 & 0 & 0 & 0 & 0 & 1 & -11.33\\ \end{array} \right]$](/images/automatica/img38.png)
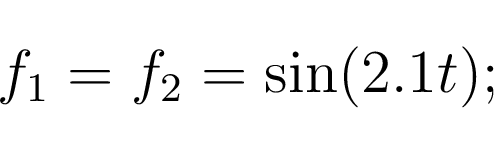
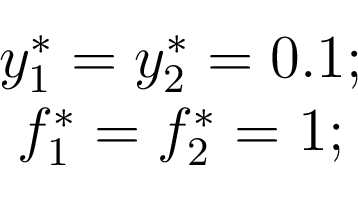
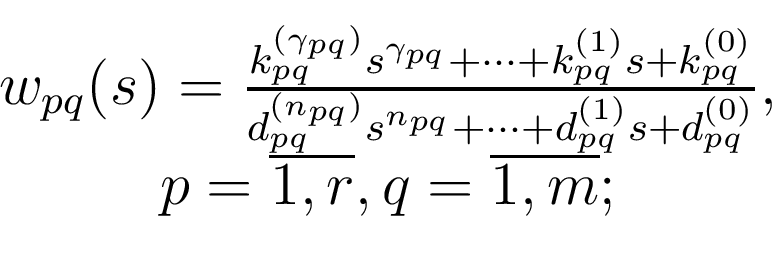
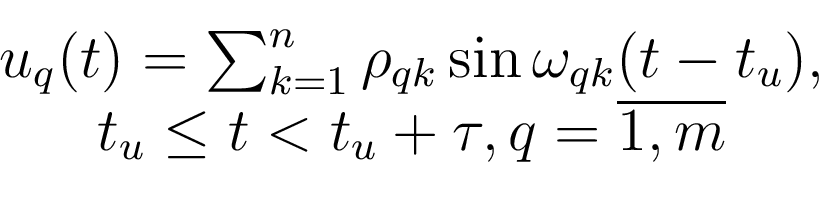
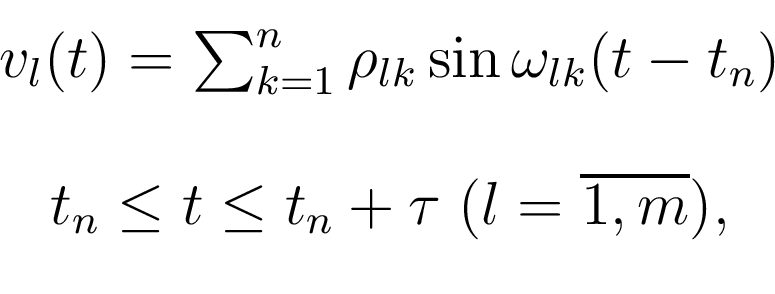
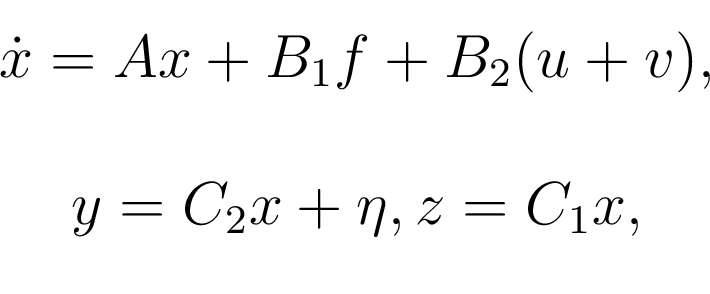

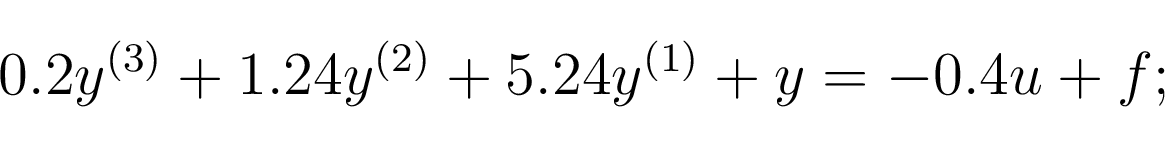
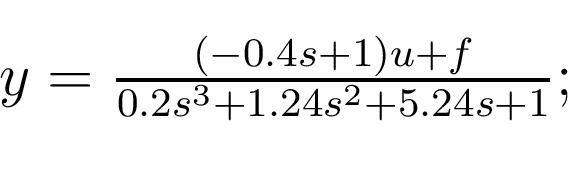
![\begin{displaymath}\begin{array}{c} f = \textmd{sign}[\sin(2.1t)]; \end{array}\end{displaymath}](/images/automatica/img71.png)